Top tips for mastering bar model drawing techniques in math instruction

Wiki Article

Exploring Bar Version Drawing Techniques: A Comprehensive Overview to Imagining Mathematics Concepts

Bar model attracting techniques act as a useful resource for both educators and students in imagining mathematical concepts. These models simplify intricate mathematical connections, aiding in the comprehension of enhancement, subtraction, multiplication, and department. This guide describes efficient approaches for applying bar models, fostering energetic involvement and real-world connections. As readers check out the practical applications and teaching pointers, they will uncover just how these methods can change their technique to maths.

Recognizing the Essentials of Bar Model Illustration

Bar design attracting works as a powerful aesthetic device in mathematics, promoting the understanding of analytical techniques and numerical relationships. This strategy includes standing for numbers and their connections via rectangle-shaped bars, making it simpler to envision procedures such as addition, subtraction, multiplication, and division. Each bar's length corresponds to a specific value, allowing students to contrast amounts and understand proportions clearly.

To produce a bar model, one starts by recognizing the trouble's crucial elements, frequently simplifying into parts that can be aesthetically represented. In a simple enhancement issue, 2 bars can be attracted, with their sizes representing the addends. The consolidated length shows the sum. In enhancement, bar models can be adjusted for extra complex problems, including fractions and ratios, by changing the bars as necessary. Grasping these essentials lays a solid foundation for effective analytical and deeper mathematical comprehension.

Advantages of Utilizing Bar Designs in Math

Utilizing bar designs in maths provides countless advantages that boost understanding and comprehension. These graphes help trainees in realizing complex ideas by damaging them down into workable components. Bar designs provide a clear structure for showing relationships between numbers, making abstract concepts much more concrete. They promote a deeper understanding of mathematical procedures and help with analytical by allowing students to visualize the data they are dealing with.

Additionally, bar versions support the development of crucial believing abilities, as trainees must assess and interpret the visual info to attract verdicts. This approach urges energetic interaction with the product, strengthening retention and mastery of mathematical principles. By fostering a strong structure in aesthetic proficiency, bar designs equip students to come close to various mathematical difficulties with self-confidence. Overall, the assimilation of bar designs into mathematics education proves valuable in growing both understanding and logical capabilities among pupils.

Using Bar Models to Enhancement and Reduction

Bar versions act as a reliable device for aesthetically representing addition and reduction troubles. By showing the connection in between numbers, they boost understanding and facilitate problem-solving. Furthermore, real-life applications of these designs can help learners grasp mathematical principles in useful contexts.

Representing Enhancement Visually

Visual help can considerably boost their understanding of these procedures when students run into addition and subtraction troubles. Bar models work as efficient tools for representing addition. By splitting a rectangle right into segments that represent the numbers involved, students can envision the connection between the amounts. If a trainee requires to include 3 and 5, they can create a bar split right into 2 areas: one section representing 3 and the various other standing for 5. This clear representation not just streamlines the addition procedure but likewise reinforces the idea of incorporating quantities. As students control these aesthetic aids, they establish a much deeper comprehension of enhancement, causing boosted analytical skills and better confidence in their mathematical abilities.

Subtraction With Bar Versions

Subtraction is typically perceived as a more complex procedure than addition, bar versions can effectively clarify this process for students. By aesthetically representing the amounts entailed, pupils can much better comprehend exactly how numbers connect to one another. In a bar model for subtraction, one bar represents the total, while one more suggests the amount being subtracted. This aesthetic distinction assists pupils comprehend the idea of "removing." If a bar reveals 10 systems, and an additional bar standing for 4 systems is gotten rid of, pupils can conveniently see that 6 systems remain. This strategy not just promotes understanding of subtraction yet likewise aids in developing problem-solving abilities, enabling students to visualize their mathematical thinking and improve their overall comprehension of mathematical principles.

Real-Life Application Instances

Understanding subtraction through bar designs lays a structure for applying these methods in real-life circumstances. In various contexts, such as budgeting or buying, people can imagine just how much cash continues to be after expenses. If a person has $50 and invests $20, a bar model can stand for the overall amount and the spent portion, showing that $30 is left. Additionally, moms and dads can utilize bar designs to aid children comprehend how lots of more products require to be contributed to finish a set, such as having three apples and requiring 5. This graph streamlines intricate troubles, promoting comprehension and retention. Inevitably, bar versions offer as effective devices in everyday decision-making, improving mathematical understanding in practical circumstances.

Visualizing Reproduction and Division With Bar Models

In exploring the application of bar designs for multiplication and department, it is necessary to comprehend their foundational concepts. Creating reproduction versions enables learners to picture relationships between numbers, while reliable department techniques can be highlighted through these aesthetic aids. This technique improves comprehension and problem-solving skills in mathematics.

Recognizing Bar Versions

Bar models work as an effective aesthetic device for showing the principles of reproduction and division. They enable click here students to stand for mathematical partnerships in an organized style, promoting a much deeper understanding of these operations. In multiplication, bar models display groups of equivalent size, enabling people to picture the total quantity when integrating these teams. On the other hand, in department, bar versions aid show just how an overall is split into smaller sized, equal parts, clarifying the concept of dividing. By employing these visual help, trainees can grasp the underlying principles of multiplication and department better. This method not only boosts understanding yet also sustains analytical abilities, making bar versions an important property in mathematical education.

Creating Reproduction Models

Building reproduction designs using bar layouts offers a clear method for visualizing the procedure of reproduction. These designs allow learners to represent multiplication as teams of equal parts, making abstract ideas more concrete. To show (3 times 4), a pupil can attract one bar divided into 3 equivalent sections, each standing for four devices. Furthermore, developing a second bar with the very same length enhances the understanding of repeated enhancement, as each sector represents one team. This graph not only help in comprehending multiplication yet also improves problem-solving skills. By using bar models, students can better comprehend relationships between numbers and develop a durable structure for more complex mathematical concepts, bring about raised confidence in their abilities.

Picturing Division Strategies

While multiplication commonly gets the limelight in early mathematics education, department is similarly crucial and can be effectively pictured using bar designs. Bar designs offer a clear graph of department issues, breaking down the procedure into manageable components. When separating a total amount right into equivalent groups, trainees can draw a long bar to stand for the whole and then section it into smaller bars that indicate each team. This method not only illustrates the concept of equivalent sharing but also reinforces the partnership between multiplication and division. By making use of bar models, students can much better comprehend division as a process of partitioning, assisting to solidify their understanding of this basic mathematical procedure.

Addressing Word Issues Utilizing Bar Design Techniques

How can aesthetic depictions boost the understanding of word troubles? Bar version methods give an effective device for pupils to damage down complicated situations right into manageable parts. By converting words into visual bars, learners can determine partnerships in between procedures and quantities more quickly. Each bar stands for a details worth, enabling trainees to see just how different elements of the issue engage.

As an example, in an issue including addition and subtraction, pupils can attract separate bars for every quantity and afterwards manipulate them to locate the solution. This procedure not only clarifies the problem however additionally promotes a much deeper conceptual understanding. Bar designs can be adjusted for various kinds of word issues, making them functional across different mathematical subjects. Eventually, using bar models can significantly enhance students' analytical skills by offering a clear aesthetic pathway to reach the correct answer.

Integrating Bar Designs in Different Mathematics Topics

Bar models can be seamlessly incorporated into different mathematics topics, boosting students' understanding of principles beyond standard arithmetic. In algebra, these aesthetic tools aid in representing inequalities and formulas, making it possible for learners to picture relationships between variables. When dealing with geometry, bar versions can illustrate the buildings of shapes and spatial thinking, aiding pupils grasp principles like area and boundary efficiently. In stats, bar designs facilitate the analysis of information sets, enabling trainees to contrast amounts and recognize patterns aesthetically. Additionally, integrating bar versions within measurement subjects aids in recognizing units and conversions by offering a concrete depiction of amounts. By using bar models across various mathematical locations, educators can promote a much deeper comprehension of intricate principles, consequently enhancing problem-solving abilities and promoting important thinking (bar model drawing techniques). This flexibility shows the utility of bar versions as a fundamental device for pupils in their mathematical trip

Tips for Training Bar Versions Properly

Incorporating bar versions right into training techniques calls for thoughtful strategies to maximize their performance. Educators needs to begin by presenting bar versions with basic, relatable instances that trainees can conveniently understand. This aids to build confidence and knowledge with the principle. Slowly boosting the intricacy of problems permits students to apply their abilities gradually. Additionally, instructors must urge students to produce their very own bar models, advertising active interaction and possession of their discovering.


Including collaborative tasks can also boost understanding, as students review and resolve issues in teams. Continual feedback is important; educators must offer positive commentary on students' bar version depictions to lead improvement. Lastly, linking bar versions to real-life scenarios enhances their relevance, aiding pupils see the functional applications of their mathematical abilities. By applying these approaches, instructors can successfully harness the power of bar designs in their mathematics instruction.

Often Asked Questions

Can Prevent Versions Be Made Use Of in Other Topics Besides Math?

Bar versions can without a doubt be utilized in numerous topics past mathematics. They effectively show concepts in scientific research, social studies, and language arts, aiding to visually represent partnerships, processes, and concepts for boosted understanding throughout disciplines.

What Age Team Is Best Suited for Understanding Bar Versions?

Bar designs are best suited for youngsters ages 7 to 12, as they develop concrete thinking skills throughout this period (bar model drawing techniques). At this age, students can effectively understand abstract concepts through aesthetic representation and problem-solving strategies

Exist Digital Tools for Creating Bar Versions?

Yes, numerous electronic devices exist for creating bar designs, consisting of academic software and online platforms. These tools help students picture mathematical principles effectively, boosting their understanding and interaction in learning with dynamic and interactive representations.

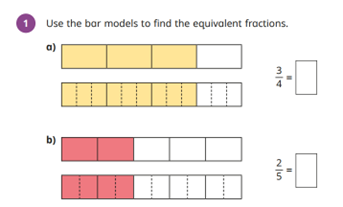
Exactly How Can I Examine Trainee Recognizing of Bar Models?

Reviewing student understanding of bar models can involve quizzes, observational assessments, and seminar. Educators could also analyze trainees' completed versions and their ability to discuss their reasoning, ensuring an extensive assessment of comprehension.

What Prevail Mistakes When Utilizing Bar Models?

Typical blunders when utilizing bar versions consist of misrepresenting quantities, falling short to accurately label bars, perplexing addition and subtraction, neglecting to make use of consistent ranges, and ignoring the relevance of clear visual separation in between different elements.

In enhancement, bar versions can be adapted for a lot more complicated issues, including portions and ratios, by adjusting the bars appropriately. Subtraction is usually viewed as a more complex operation than addition, bar models can effectively clarify this procedure for trainees. In a bar model for subtraction, one bar stands for the total, while one more shows the quantity being deducted. If a bar shows 10 units, and one more bar representing 4 devices is eliminated, students can conveniently see that 6 systems continue to be. When dividing a total amount right into equal groups, trainees can attract a long bar to represent the whole and after that segment it into smaller bars that suggest each team.

Report this wiki page